[next] [prev] [prev-tail] [tail] [up]

C.  Berechnung des Integrationsanteils A

In Abschnitt  4.3.1 wurde der Integrationsanteil A eingeführt und im Detail erklärt. Er stellt bei der Berechnung des Tunnelstroms für die Simulation der Kontrastinversion ein Maß dafür dar, wie schnell die numerische Summation der Teilströme abgebrochen wird. An dieser Stelle soll die Gleichung  4.6
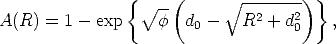
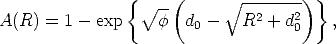{ ( )} V~ -- V~ -------2 A(R) = 1- exp f d0 - R2 + d 0 ,
(C.1)

die eine Beziehung zwischen dem Anteil A und dem Integrationsradius herstellt, hergeleitet werden.

Der Anteil A ist das Verhältnis

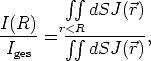integral integral dSJ (r) I(R)- = r< integral R integral --------, Iges dSJ (r)
(C.2)

wobei

2 V~ ---- J (s) = e--2mfU----.exp( -AsV ~ f) h2s
(C.3)

gilt (siehe Gl.  2.9).

J hängt also nur von s = 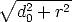V~ ------- d20 + r2 ab, weswegen wir zur Berechnung der gemeinsamen Stammfunktion beider Integrale Polarkoordinaten benutzen —was zu dS = 2pr dr = 2ps ds führt— und dabei die Konstanten vergessen, da sie ohnehin gekürzt würden:

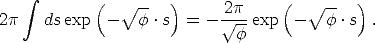integral ( V~ -- ) ( V~ -- ) 2p dsexp - f .s = - 2 V~ p--exp - f .s . f
(C.4)

Einsetzen der Integrationsgrenzen in Gl.  C.4 liefert

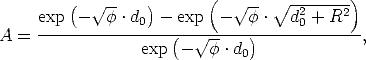( V~ -- ) ( V~ -- V~ --------) exp - f .d0 - exp - f . d20 + R2 A = ----------------(-- V~ -----)-------------, exp - f .d0
(C.5)

was sich natürlich zum bekannten Ergebnis

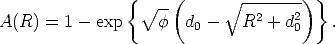{ -( V~ --------)} A(R) = 1- exp V~ f d - R2 + d2 . 0 0
(C.6)

vereinfachen läßt.

[next] [prev] [prev-tail] [front] [up]