|
|
Die Tatsache, daß entgegen der Vorhersage der klassischen Physik überhaupt ein Strom durch eine Potentialbarriere fließt, läßt sich auf verschiedene Weise erklären. Zum Beispiel kann man zeigen, daß die Verweildauer eines Teilchens in einer eindimensionalen rechteckigen Barriere immer kleiner ist als h/(V - E) (siehe Abb. 2.3),

welche besagt, daß das Produkt der Energiemeßgenauigkeit  E mit dem Meßfehler
der Zeit
E mit dem Meßfehler
der Zeit  t immer größer als h ist, nicht mit Sicherheit ausschließen kann, daß das
Teilchen gleichzeitig eine Energie E < V habe und sich zwischen x = 0 und x = L
aufhalte.
t immer größer als h ist, nicht mit Sicherheit ausschließen kann, daß das
Teilchen gleichzeitig eine Energie E < V habe und sich zwischen x = 0 und x = L
aufhalte.
Beim Beispiel der rechteckigen Potentialbarriere bleibend läßt sich der Teilchentransfer von links nach rechts auch durch einfaches Lösen der stationären Schrödingergleichung

berechnen. Die Transmissionswahrscheinlichkeit lautet für den Fall E < V 0 (siehe z.B. [2] oder [27])
![[ ]-1
-----sinh2-kL------
T = 1 + 4(E/V )(1 - E/V ) ,
0 0](main6x.jpg)
wobei k = 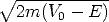 /h ist. Bei Treppenfunktionspotentialen mit endlich vielen
Stufen läßt sich die Transfermatrixmethode [23] anwenden.
/h ist. Bei Treppenfunktionspotentialen mit endlich vielen
Stufen läßt sich die Transfermatrixmethode [23] anwenden.
| Notation: | |
| m | Teilchenmasse |
| V 0 | Barrierenhöhe |
| L | Barrierenlänge |
| E | Teilchenenergie |
Legt man an besagte Elektroden eine Spannung an, so fließt aufgrund des quantenmechanischen Tunneleffekts ein Elektronenstrom.
| Notation: | |
| m | Elektronenmasse |
| e | Elektronenladung |
| V (x) | Potential der Barriere |
| EF | Fermienergie |
| U | an den Elektroden anliegende Spannung |
| J | Tunnelstromdichte |
| f(E) | Fermi-Dirac-Funktion |
| s1,s2 | Stellen, an denen V = EF gilt |
 s s | = s2 - s1, Breite der Barriere |
 | mittlere Barrierenhöhe |
| vm | maximale Geschwindigkeit der Elektronen |
| Em | maximale Energie der Elektronen |
|
|
 | (2.1) |
wobei n(vx)dvx die Anzahl der Elektronen pro Einheitsvolumen ist, deren Geschwindigkeit in x-Richtung zwischen vx und vx + dvx liegt, und T(Ex) die Tunnelwahrscheinlichkeit gemäß der WKB-Näherung (nach Wentzel, Kramers und Brillouin benannt), die u.a. in [24] beschrieben wird:
![( s2 )
2 integral 1
T(Ex) = exp - -- dx [2m(V (x) - Ex)]2 .
hs
1](main11x.jpg) | (2.2) |
Die Elektronen im Metall werden als freies Gas angenommen, so daß ihre
Zustandsdichte im 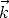 -Raum 2
-Raum 2 , und im
, und im  -Raum 2
-Raum 2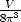
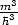 (wegen h
(wegen h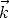 = m
= m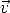 ) ist.
Die Anzahl der Elektronen pro Einheitsvolumen in einem infinitesimalen
Geschwindigkeitsintervall ist daher
) ist.
Die Anzahl der Elektronen pro Einheitsvolumen in einem infinitesimalen
Geschwindigkeitsintervall ist daher
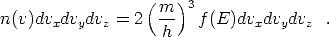 | (2.3) |
Über die Geschwindigkeitskomponenten parallel zur Oberfläche muß also noch integriert werden. Aus Gl. 2.3 erhält man dabei
 | (2.4) |
mit E|| =  m(vy2 + v
z2).
m(vy2 + v
z2).
Nun kann Gleichung 2.4 in Gl. 2.1 eingesetzt werden:
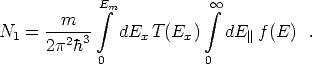
Die Anzahl der Elektronen, die in Abbildung 2.4 von rechts nach links fließen, läßt sich ähnlich bestimmen. Dabei ist zu beachten, daß die Tunnelwahrscheinlichkeit T unabhängig von der Richtung ist, die Fermi-Dirac-Funktion nun aber als Funktion von E + eU genommen werden muß, also
 | (2.5) |
Bei U 0 erhält man eine resultierende Ladungsstromdichte J = e
0 erhält man eine resultierende Ladungsstromdichte J = e N mit
N mit
 N = N1 - N2.
N = N1 - N2.
Aus der Abbildung 2.4 geht hervor, daß V (x) = EF + 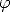 . Diese Substitution wird
in in Gl. 2.2 eingesetzt. Nach Einführung der mittleren Barrierenhöhe
. Diese Substitution wird
in in Gl. 2.2 eingesetzt. Nach Einführung der mittleren Barrierenhöhe
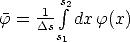 , zeigt Simmons, daß in guter Näherung
, zeigt Simmons, daß in guter Näherung
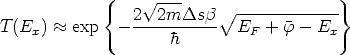 | (2.6) |
gilt, was in Anhang A.1 gezeigt wird, wo auch die Definition des Korrekturfaktors
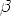 zu finden ist. Dieser beträgt für kleine Spannungen (U «
zu finden ist. Dieser beträgt für kleine Spannungen (U «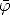 /e) ungefähr eins.
Wenn man zusätzlich die Fermi-Dirac-Funktion durch eine Stufenfunktion annähert,
was aufgrund der hohen Fermitemperatur (T « TF ) der Elektronen in Metallen
gerechtfertigt ist, erhält man für J nach einigen einfachen Umformungen (siehe
Anhang A.2) folgenden Ausdruck, in dem Gleichung 2.6 bereits berücksichtigt ist:
/e) ungefähr eins.
Wenn man zusätzlich die Fermi-Dirac-Funktion durch eine Stufenfunktion annähert,
was aufgrund der hohen Fermitemperatur (T « TF ) der Elektronen in Metallen
gerechtfertigt ist, erhält man für J nach einigen einfachen Umformungen (siehe
Anhang A.2) folgenden Ausdruck, in dem Gleichung 2.6 bereits berücksichtigt ist:
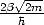 gesetzt. Nach einigen Näherungen bei der Integration von
Gl. 2.7, die in Anhang A.2 detailliert durchgeführt wird, erhält man
gesetzt. Nach einigen Näherungen bei der Integration von
Gl. 2.7, die in Anhang A.2 detailliert durchgeführt wird, erhält man
Gleichung 2.8 bietet einerseits die Möglichkeit, die Tunnelstromdichte ohne die
genaue Kenntnis des Barrierenverlauf 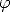 (x) zu berechnen —lediglich die mittlere
Barrierenhöhe
(x) zu berechnen —lediglich die mittlere
Barrierenhöhe 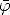 muß bekannt sein—, andererseits erlaubt sie aber auch, aufgrund
einer gemessenen Strom-Spannungs-Charakteristik die mittlere Barrierenhöhe
muß bekannt sein—, andererseits erlaubt sie aber auch, aufgrund
einer gemessenen Strom-Spannungs-Charakteristik die mittlere Barrierenhöhe  zu
bestimmen.
zu
bestimmen.
Der erste Term in Gleichung 2.8 kann als Stromdichte aufgefaßt werden, die von nach rechts tunnelnden Elektronen herrührt, der zweite als diejenige der nach links tunnelnden Elektronen. Die Differenz ergibt die Gesamtstromdichte.
Für kleine Spannungen läßt sich Gl. 2.8 weiter zu
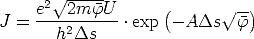 | (2.9) |
vereinfachen, wie ebenfalls in Anhang A.2 gezeigt wird. Dabei wird im Ausdruck
für A der Faktor 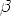 gleich Eins gesetzt, also A =
gleich Eins gesetzt, also A = 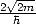 .
.
Die exponentielle Abhängigkeit vom Abstand  s zwischen der Tunnelspitze und
der Probenoberfläche ist wesentlich für den Tunnelvorgang: da der Wert von
A .
s zwischen der Tunnelspitze und
der Probenoberfläche ist wesentlich für den Tunnelvorgang: da der Wert von
A . beim Tunnelmikroskop üblicherweise im Bereich 1 Å-1
–2 Å-1 liegt,
variiert der Strom schon über Größenordnungen, bei Abstandsänderungen im
Ångstrøm-Bereich. Außerdem weist Gl. 2.9 einen Ohmschen Zusammenhang
zwischen Strom und Spannung auf.
beim Tunnelmikroskop üblicherweise im Bereich 1 Å-1
–2 Å-1 liegt,
variiert der Strom schon über Größenordnungen, bei Abstandsänderungen im
Ångstrøm-Bereich. Außerdem weist Gl. 2.9 einen Ohmschen Zusammenhang
zwischen Strom und Spannung auf.
Die Tersoff-Hamann-Theorie basiert auf der zeitabhängigen Störungstheorie. Mittels Fermi’s Goldener Regel läßt sich der Tunnelstrom nämlich folgendermaßen schreiben:
![sum 2
I = (2pe/h) f(Em)[1 - f(En + eU)]|Mmn |d(Em - En).
mn](main36x.jpg) | (2.10) |
| Notation: | |
| U | angelegte Spannung |
| f(E) | Fermi-Dirac-Funktion |
M  | Tunnelmatrixelement zwischen Spitzenzustand 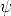  |
und Oberflächenzustand 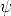  |
|
E | Energie des Zustandes 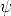  |
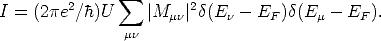 | (2.11) |
EF ist dabei die Fermienergie. Das Hauptproblem stellt die Berechnung des
Matrixelements M
 dar. Bardeen [1] hat gezeigt, daß
dar. Bardeen [1] hat gezeigt, daß
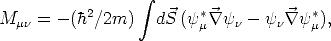 | (2.12) |
wobei die Integrationsfläche komplett zwischen den Elektroden, also innerhalb der Barriere, liegen muß.
Es werden also Ausdrücke für sowohl die Spitzenfunktion 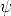
 als auch die
Oberflächenfunktion
als auch die
Oberflächenfunktion 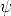
 benötigt. Die letztere kann zunächst in eine Fourrierreihe entwickelt
werden.2
Erstere ist jedoch im allgemeinen unbekannt. Sie wird im Modell von Tersoff und
Hamann als Kugelwelle angenommen, mit dem Mittelpunkt
benötigt. Die letztere kann zunächst in eine Fourrierreihe entwickelt
werden.2
Erstere ist jedoch im allgemeinen unbekannt. Sie wird im Modell von Tersoff und
Hamann als Kugelwelle angenommen, mit dem Mittelpunkt  0 (siehe Abbildung
2.5).
0 (siehe Abbildung
2.5).
|
|
 0) wird vernachlässigt.
0) wird vernachlässigt.
Auf diese Weise erhalten sie bis auf einige konstante Faktoren folgenden Ausdruck für den Strom I:
 | (2.13) |
Dabei ist DS(EF ) die Zustandsdichte an der Fermikante für die Spitze,
k = 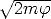 /h die reziproke Abklinglänge der Wellenfunktion im
Vakuum,
/h die reziproke Abklinglänge der Wellenfunktion im
Vakuum, 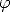 die lokale Barrierenhöhe und R der effektive Radius der
Spitze. Die Summe identifiziert man leicht als lokale Zustandsdichte
(LDOS3)
der Probenoberfläche an der Fermienergie. Nach dieser Theorie werden bei der
Rastertunnelmikroskopie also Abbilder von Flächen konstanter LDOS an der
Fermikante erzeugt.
die lokale Barrierenhöhe und R der effektive Radius der
Spitze. Die Summe identifiziert man leicht als lokale Zustandsdichte
(LDOS3)
der Probenoberfläche an der Fermienergie. Nach dieser Theorie werden bei der
Rastertunnelmikroskopie also Abbilder von Flächen konstanter LDOS an der
Fermikante erzeugt.
Zwar hat der Wert der Oberflächenwellenfunktion am Ort 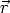 0 keine physikalische
Relevanz —das Matrixelement ist durch eine Integration vollständig innerhalb der
Isolatorregion bestimmt—, doch beschreibt die formale Berechnung von
0 keine physikalische
Relevanz —das Matrixelement ist durch eine Integration vollständig innerhalb der
Isolatorregion bestimmt—, doch beschreibt die formale Berechnung von 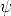
 im
Abstand R + d auf korrekte Weise die laterale Mittelung aufgrund der endlichen
Spitzenausdehnung.
im
Abstand R + d auf korrekte Weise die laterale Mittelung aufgrund der endlichen
Spitzenausdehnung.
Der exponentielle Abfall von 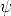
 senkrecht zur Probenoberfläche
senkrecht zur Probenoberfläche
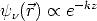
wirkt sich damit direkt auf den Strom I aus, denn der ist zum Betragsquadrat der
Oberflächenzustände am Ort  0 proportional, woraus
0 proportional, woraus
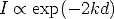 | (2.14) |
folgt. Der Strom gehorcht also auch hier, so wie in der eindimensionalen Betrachtung, der exponentiellen Abhängigkeit vom Abstand und der Wurzel aus der effektiven Barrierenhöhe.
Gute quantitative Übereinstimmung mit STM-Experimenten auf einer 2 × 1-rekonstruierten Gold-(110)-Oberfläche [39] war der erste Erfolg dieser Theorie. Rechnungen für dieses Beispiel ergaben eine laterale Auflösung von 5 Å, womit die Periodizität von 8 Å beobachtet werden kann.
Jedoch wurden bald entscheidende Mängel der Tersoff-Hamann-Theorie erkannt. Sie war vor allen Dingen nicht in der Lage, die atomare Auflösung zu erklären, was unter anderem mit dem Ausschluß der p- und d-Zustände zusammenhängt. So zeigten Ohnishi und Tsukada 1989 mit ihrer Molekülorbitaltheorie [30], daß die dz2-Zustände des Spitzenatoms einer Wolframnadel den dominanten Beitrag zum Tunnelstrom geben. Sie machten dabei verschiedene Modellannahmen für Wolframcluster am Ende der Nadel, mit denen First-Principles-Rechnungen durchgeführt wurden, wobei sich herausstellte, daß die dz2-Zustände eine stark gerichtete und weite Ausdehnung haben und energetisch nahe an der Fermikante liegen.
Ein wichtiges Problem stellt außerdem die gegenseitige Beeinflussung von Probe und Spitze dar. Bardeen ist bei der Berechnung des Tunnelmatrixelements von ungestörten Wellenfunktionen ausgegangen. Dies ist nur bei genügend großen Abständen zwischen den Elektroden gerechtfertigt, d.h. ab einem Abstand von ca. 6 Å, ab dem die atomare Korrugation allerdings verschwindet [13]. Auf Profile großer Überstrukturen wie z.B. eben denen auf Au(110) oder auf einzelne, auf glatten Metalloberflächen adsorbierte Atome, wie es in [25] beschrieben wird, ist die Theorie jedoch gut anwendbar.
1993 stellte Chen in [13] die Modifizierte Bardeen-Theorie (MBA4) vor, in der er die Vorgehensweise von Bardeen abwandelte. Dabei waren folgende Erfordernisse zu erfüllen:
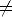 0.
0.
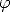 keine Voraussetzung mehr sein.
keine Voraussetzung mehr sein.
Chen hat gezeigt, daß Bardeens Übergangsmatrixelement selbst bei verschwindender oder sogar negativ werdender Barriere durchaus korrekte Ergebnisse liefert, sofern man die richtig modifizierten Wellenfunktionen einsetzt.
Für die störungstheoretische Behandlung wurde, wie in Abbildung 2.6a
|
|
 | (2.15) |
das heißt, daß in der Spitzenregion US = 0 und in dem Bereich der Oberfläche UT = 0 gilt. Also gilt die weitere Relation6
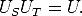 | (2.16) |
Abb. 2.6b zeigt den Verlauf von U sowie die Energien der beiden Zustände. In
den beiden unteren Diagrammen der Abbildung 2.6 ist zu erkennen, daß die
Potentiale US und UT den jeweils zugehörigen ungestörten Potentialen US0
und UT0 gegenüber in der Barrierenregion verringert sind. Die jeweilige
Differenz zwischen gestörtem und ungestörtem Potential wird als Störung
behandelt. Mit diesen Störpotentialen kann dann zeitabhängige Störungstheorie
betrieben werden, mit der man in erster Ordnung (Fermi’s Goldene Regel) die
Übergangswahrscheinlichkeit für ein Elektron vom Oberflächenzustand 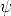
 in den
Spitzenzustand
in den
Spitzenzustand 

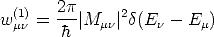 | (2.17) |
erhält.
Das Matrixelement
 | (2.18) |
hat hier die gleiche Form wie das der Bardeen-Theorie, doch müssen nun die modifizierten Wellenfunktionen eingesetzt werden. Es hat die Dimension einer Energie. Chen hat gezeigt, daß die Bedeutung dieses Übergangsmatrixelements gerade der Verringerung der Tunnelbarriere durch die Überlappung der beiden Wellenfunktionen, also der Austauschwechselwirkung, entspricht.
Der Effekt des Störpotentials, z.B. V  US -US0, kann mittels der Dyson-Gleichung
in erster Ordnung
US -US0, kann mittels der Dyson-Gleichung
in erster Ordnung
 | (2.19) |
berechnet werden. Dabei sind 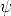 0 und
0 und 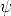 jeweils die ungestörte beziehungsweise die
gestörte Wellenfunktion. Die Greensche Funktion G(
jeweils die ungestörte beziehungsweise die
gestörte Wellenfunktion. Die Greensche Funktion G(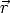 ,
,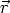 ') ist durch
') ist durch
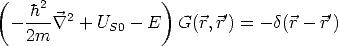 | (2.20) |
definiert.
Zur Überprüfung wurde die MBA auf analytisch lösbare Fälle angewandt, nämlich auf das Problem der eindimensionalen rechteckigen Potentialbarriere (siehe Abb. 2.3) sowie auf das Elektron im Wasserstoffmolekülion. In beiden Rechnungen erreicht die Modifizierte Bardeen-Theorie eine hohe Genauigkeit, selbst wenn die Barriere verschwindet oder sogar niedriger als die Teilchenenergie wird. Da die Rechnungen lang und aufwendig sind, werden sie hier nicht aufgeführt; es sei dazu nur auf den ausführlichen Aufsatz von Chen [13] verwiesen.
Für die Anwendung der MBA auf das STM hat Chen explizite Ausdrücke für das Übergangsmatrixelement berechnet, indem er die Wellenfunktionen der Spitze in Kugelflächenfunktionen entwickelte und mit ihnen die Schrödingergleichung löste. Einsetzen einer beliebigen Spitzenfunktion mit einem Bahndrehimpuls bis zu l = 2 sowie der Probenfunktion in Gl. 2.18 lieferte einen Ausdruck für das Matrixelement, der als Linearkombination von partiellen Ableitungen der Probenfunktion am Mittelpunkt des Spitzenatoms geschrieben werden kann.
Dieses Resultat faßte Chen [9] zusammen in der sogenannten Derivative Rule: man schreibe die Spitzenwellenfunktion in Abhängigkeit von x, y und z, nehme folgenden Ersatz vor:
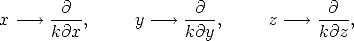 | (2.21) |
wende diese Ableitungen auf die Probenwellenfunktion an und erhalte somit das gewünschte Übergangsmatrixelement. k ist wie in Abschnitt 2.2.2 definiert. Zu den detaillierten Rechnungen und Ergebnissen sei wiederum auf [13] verwiesen.
Mittels dieser Regel lassen sich die zu verschiedenen Orbitalen gehörenden
Matrixelemente einfach berechnen. Da das Betragsquadrat dieser Elemente
proportional zur Tunnelleitfähigkeit ist, erhält man somit die Leitfähigkeitsverteilung
 (
(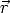 ).
).
Bemerkenswert ist dabei, daß man das gleiche Tunnelmatrixelement erhält, wenn
man die Probenwellenfunktion mit der Spitzenwellenfunktion vertauscht. So ist
 (
(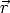 ) z.B. sowohl im Falle eines s-Orbitals an der Spitze und dz2-Zuständen
an der Probenoberfläche als auch im umgekehrten Fall proportional zu
(3 cos 2
) z.B. sowohl im Falle eines s-Orbitals an der Spitze und dz2-Zuständen
an der Probenoberfläche als auch im umgekehrten Fall proportional zu
(3 cos 2 - 1)2e-2
- 1)2e-2 r. Diese Tatsache wird das Reziprozitätsprinzip genannt [8].
Man kann ein STM-Bild also derart interpretieren, daß das Probenorbital
mit dem Spitzenorbital abgetastet wird, oder das Spitzenorbital mit dem
Probenorbital. Eine Illustration zu diesem Resultat zeigt Abbildung 2.7.
r. Diese Tatsache wird das Reziprozitätsprinzip genannt [8].
Man kann ein STM-Bild also derart interpretieren, daß das Probenorbital
mit dem Spitzenorbital abgetastet wird, oder das Spitzenorbital mit dem
Probenorbital. Eine Illustration zu diesem Resultat zeigt Abbildung 2.7.
|
SPITZE, dz2 SPITZE, s
|
Außerdem zeigte der Vergleich der Matrixelemente für Wellenfunktionen verschiedener l-Quantenzahlen (0 < l < 2), daß hohe Werte für l ein Vielfaches der atomaren Korrugation, die die Flächen gleicher lokaler Zustandsdichte (LDOS) aufweisen, ergeben. Damit konnte erstmals eine plausible Erklärung für extrem große mit dem STM gemessene Korrugationsamplituden von bis zu 8 Å auf der Aluminium-(111)-Fläche, die vorerst nicht mit den Resultaten von First-Principles-Rechnungen oder Heliumstreuexperimenten, welche eine Amplitude von nur 0,03 Å für die Fläche gleicher LDOS im Abstand von 3 Å aufzeigen, zu vereinbaren gewesen waren, gegeben werden.
An dieser Stelle seien die wichtigsten Ergebnisse, die sich aus der störungstheoretischen Behandlung des Tunnelproblems von Chen ergeben haben, aufgelistet:
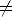 0. Dies ist wichtig, da aufgrund verschiedener Modellrechnungen
(siehe z.B. [30]) zu vermuten ist, daß d-Zustände an Spitzenatomen eine
größere Reichweite haben als von Tersoff und Hamann angenommen.
0. Dies ist wichtig, da aufgrund verschiedener Modellrechnungen
(siehe z.B. [30]) zu vermuten ist, daß d-Zustände an Spitzenatomen eine
größere Reichweite haben als von Tersoff und Hamann angenommen.
Zum Schluß sollte erwähnt werden, daß es außer der modifizierten Bardeen-Theorie von Chen auch andere Theorien gibt, die von der Bardeen-Näherung abweichende Ansätze haben, wie z.B. den streutheoretischen Ansatz von Doyen in [15] oder die Berechnungen von Noguera in [29] mittels Greenscher Funktionen, die die Kopplung beider Elektroden vollständig mit einbeziehen.