|
|
Es wurden mit dem AFM bereits viele verschiedene Erscheinungen im Zusammenhang mit atomarer Reibung beobachtet, die grob in zwei Kategorien unterteilt werden können: zum einen gibt es sogenannte Einlaufstreifen und atomare Stick-Slips, die in einzelnen Rasterzeilen auftreten und daher als eindimensionale Reibungsphänomene bezeichnet werden, zum anderen gibt es viele weitere Effekte, die erst im Gesamtbild sichtbar werden und daher zweidimensionale Reibungsphänomene genannt werden. Eine solche Unterteilung ist auch beim STM sinnvoll.
|
|
Bilder mit ähnlichem Charakter wurden vielfach mit dem AFM erzeugt [34]. Da der schnelle, fast unstetige Sprung des entsprechenden Signals ein „Zurückschnellen“ der Feder beim AFM bedeutet, wird dieses sägezahnförmige Profil im allgemeinen derart interpretiert, daß die Spitze im Bereich der größten Steigung des Potentials „haften“ bleibt (stick), um im nächsten Moment, in dem die Federspannung einen Schwellenwert erreicht, einen Gitterplatz weiterzuspringen (slip3), woher der Begriff „Stick-Slip“ stammt.
Wird die Abtastrichtung gegenüber den atomaren Reihen etwas gedreht, so erhält man zusätzlich zu den atomaren Stick-Slips auch sogenannte Reihen-Stick-Slips: beim Durchlauf einer Zeile springt die Spitze nach einer gewissen Anzahl A von Gitterplätzen zu einer jeweils neuen atomaren Reihe. Wenn man den Winkel entsprechend wählt, kann diese Anzahl eine natürliche Zahl sein, wodurch der Querschnitt eine Periodizität erhält. Dies kann mit den Eigenbau-Rasterkraftmikroskopen der Arbeitsgruppe gezielt praktiziert werden, mit dem kommerziellen STM jedoch nicht, da der Winkel hier nur in 15°-Schritten einstellbar ist. Abbildung 6.2
|
|
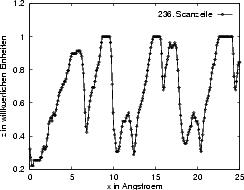
Wie schon auf Seite 148 erwähnt, kann auch die Orientierung der Nadel im Bezug zur Scanrichtung einen entscheidenden Einfluß auf den Bildcharakter haben. Dies soll hier kurz anhand dreier kurz hintereinander gemessener STM-Bilder, die in Abbildung 6.3
|
a)
d)
|
3, wie der
Querschnitt der 236sten Scanzeile zeigt—, verlaufen die Diskontinuitäten in den
weiteren beiden Bildern, die mit einem Winkel von jeweils ±60° gegenüber dem
ersten Bild aufgenommen wurden, in andere Richtungen, was ihnen eine andere
Struktur verleiht. Da solche Drehungen das hexagonale Gitter identisch
abbilden, kann für diesen Effekt nur eine Asymmetrie der Spitze verantwortlich
sein.
Bei den Untersuchungen mit dem STM wurde noch eine besondere Variation der Stick-Slip-Prozesse beobachtet, die im folgenden dargestellt werden soll: auf Wolframdiselenid (WSe2) wurden nach kleinen apparativen Modifikationen sowohl Hinlauf als auch Rücklauf simultan aufgenommen. Da dies im Park-System nicht vorgesehen war, gibt es allerdings auch eine kleine Einschränkung: es ist nur der Betrieb im CHI-Modus sinnvoll. Dabei wurden Resultate wie die in Abbildung 6.4
|
a)
|
|
|
Die Kurve 6.4c zeigt allerdings nicht nur eine Hysterese, es fällt auch auf, daß im Hinlauf schmale Strommaxima, im Rücklauf dagegen schmale Minima auftauchen. Wie man anhand der Bilder 6.4a und b sieht, ist dies in allen Zeilen der Fall.
Wenn man davon ausgeht, daß wie beim AFM laterale Kräfte für diese
Stick-Slip-Prozesse verantwortlich sind, so sollte hier noch zusätzlich versucht
werden, mögliche Zusammenhänge zwischen dem gemessenen Strom und den
anzunehmenden Kräften aufzuzeigen. Ein erster Erklärungsversuch könnte auf der
schon auf Seite 159 angedeuteten Verbiegung der Spitze basieren. Eine solche kann
nämlich dazu führen, daß sich die Orientierung der Spitze gegenüber der
Probenoberfläche derart ändert, daß die Art der Elektronenorbitale, die das
„Hängenbleiben“ des untersten Teils der Spitze an den Probenatomen verursachen,
wechselt. Denn nicht Elektronen aller Zustände können zum Tunnelstrom beitragen,
nur diejenigen mit einem Wellenvektor k
kF , d.h. nahe der Fermioberfläche.
Wechselwirkungskräfte involvieren dagegen Elektronen des gesamten Impulsraums
(k < kF ) [17]. Mit anderen Worten könnte auf die vordere Flanke der relevanten
Spitzenatome beim Hinlauf eine repulsive Kraft wirken, die einerseits eine
Weiterbewegung der Spitze verhindert, aber auch eine für hohen Tunnelstrom
förderliche Überlappung geeigneter Orbitale, wie z.B. zwischen x = 5 Å
und x = 9 Å in der 127sten Scanzeile (Abb. 6.4c). Dieser Zustand hält
an, bis ein Schwellenwert der Auslenkung, der durch die Elastizität der
Nadel gegeben ist, überschritten wird. An diesem springt die Spitze zum
nächsten Gitterplatz, wobei die Verbiegung kurzfristig nachläßt und ein
höherer Tunnelstrom möglich wird. Beim Rücklauf erfährt ein anderer
Spitzenzustand die größte Annäherung an die Probe. Dieser könnte während der
Stick-Phase einen hohen Tunnelstrom bedingen, zum Zeitpunkt des Slip
hingegen tritt eine ähnliche Situation ein wie bei der Slip-Phase des Hinlaufs.
Dies würde auch erklären, wieso die Maxima des Hinlaufs auf ähnlichem
Niveau liegen wie die Minima des Rücklaufs, was in den anderen Scanzeilen
ebenfalls mehr oder weniger der Fall ist. Die Abbildungen 6.6a und b
Wenn man als andere Möglichkeit von der Vorstellung einer Verbiegung der
Spitze absieht, also zulassen würde, daß beide, für den Hin- und Rücklauf
relevanten Orbitale immer den gleichen Abstand zur Probenoberfläche hätten, so
müßte gewährleistet sein, daß das jeweils nicht an der lateralen Kraft beteiligte
Orbital sich während der Stick-Phase innerhalb einer Potentialmulde befände, also
ca. eine halbe Gitterkonstante vom anderen entfernt. Da solch eine kurze Distanz
zwischen den Orbitalen allerdings unwahrscheinlich ist, wäre in diesem Fall
zu vermuten, daß sie zwar weiter auseinanderliegen, die Projektion ihrer
Entfernung auf die x-Achse, also die Scanrichtung, aber bis auf ein Vielfaches
der Gitterkonstanten g ungefähr 
g entspricht: eine „Nano-Doppelspitze“
also.
Etwas längere Einlaufstreifen von etwa 10–15 Ångstrøm zeigt Abbildung 6.7
|
a)
|
Einen möglichen Erklärungsansatz würden wiederum die Überlegungen zu den Stick-Slip-Prozessen liefern. Bei ansteigendem Strom könnte es sich um eine wie die in Bild 6.6a dargestellte Situation handeln: Mit fortschreitender Bewegung der Probe relativ zur Nadelhalterung steigt die repulsive laterale Kraft, was zu einer weiteren Annäherung beider Elektronenorbitale führt, wodurch sich der Tunnelstrom erhöht. Abfallenden Strom könnte dagegen Bild 6.6b veranschaulichen: Hier wirkt durch die teilweise Überlappung beider Orbitale eine attraktive laterale Kraft. Im Verlauf der Scanbewegung vergrößert sich daher ihr Abstand, was zu einer Verringerung des Tunnelstroms führt.
In Bild a der Abbildung 6.7 zeigen die Einlaufstreifen in den meisten Scanzeilen noch eine Besonderheit: Jeweils zu Beginn —also ganz links, da es sich um den Hinlauf handelt— treten Diskontinuitäten im Tunnelstrom auf, bevor der eigentliche Einlaufstreifen beginnt. Eine mögliche Erklärung liegt darin, daß sich die Spitze in diesen Fällen zu Beginn einer Scanzeile vermutlich noch gar nicht in einer Potentialmulde befindet, sondern erst nach Fortschreiten des Scanvorgangs um bis zu etwa einer halber Gitterkonstanten, wo die für den Einlaufstreifen verantwortliche laterale Kraft einsetzt. Eine andere Besonderheit erkennt man in den STM-Bildern jeweils gegenüber von den Einlaufstreifen, also beim Hinlauf im rechten Rand, beim Rücklauf im linken. Diese senkrechten Streifen, die keine Fortsetzung der atomaren Struktur zeigen, haben ihre Ursache mit hoher Wahrscheinlichkeit in einem Fehler im Meßprogramm.
Überaschenderweise werden die Einlaufstreifen zum Teil mehrere Nanometer lang, wie man anhand der in Abbildung 6.8
Die in Abbildung 6.8 zu betrachtenden STM-Bilder wurden auf WSe2 aufgenommen, bis auf das letzte (Bild f), welches auf MoS2 entstand.
Es hat sich herausgestellt, daß die Länge der Einlaufstreifen zum Teil vom Strom, d.h. vom Spitze-Probe-Abstand, abhängig ist: So wie man es erwarten würde, sind sie bei kleinen Abständen länger als bei großen, wie es der Vergleich der ersten beiden Spalten der Abbildung 6.8 verdeutlicht. Jedoch war diese Abhängigkeit nur kurzfristig reproduzierbar, da sich die untersten Spitzenatome vermutlich in einem labilen Zustand befanden, wobei das Wort Zustand hier den sowohl elektronischen als auch den geometrischen meint. Bild e entstammt z.B. einer Messung mit derselben Spitze, doch einige Stunden früher; es wurden bei einem sehr viel höheren Strom kürzere Einlaufstreifen registriert.
Viel prägnanter ist die Abhängigkeit von den Scanwinkeln: Die Bilder a und c wurden bei ähnlichen Abtastrichtungen erzeugt, b und d bei um ca. 90° dazu gedrehten. Bei der Aufnahme von Bild e wurde diese Drehung nach etwa dem ersten Fünftel des Durchlaufs durchgeführt. Da diese Winkelabhängigkeit gut und sogar über mehrere Tage hinweg —mit derselben Spitze jedoch an unterschiedlichen Probenstellen— reproduzierbar war, liegt es nahe anzunehmen, daß hierfür eine makroskopische Eigenschaft der Tunnelnadel verantwortlich war, nämlich eine Anisotropie der Elastizität, da vermutlich die Elastizität der Nadel in Scanrichtung für die Ausprägung der Einlaufstreifen verantwortlich ist. Während die Nadel in der einen Richtung sehr elastisch ist, also eine kleine Federkonstante k hat, und dadurch zu Beginn jeder Scanzeile um große Strecken ausgelenkt wird, bewirkt eine größere Federkonstante in einer dazu senkrechten Richtung einen kleineren Einlaufstreifen.
Da bei einigen Messungen extrem lange Einlaufstreifen beobachtet wurden, die auf Molybdändisulfid sogar fast hundert Ångstrøm erreicht haben (siehe Abbildung 6.8f), stellte sich die Frage, in welcher Größenordnung die Federkonstante liegen muß, um solche Effekte zu erhalten. Der nächste Abschnitt befaßt sich kurz damit.
= 
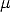im atomaren Bereich
in der gleichen Größenordnung wie der makroskopische liegt, kann man
diesen mit 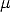0,1 abschätzen, woraus als sehr grobe Abschätzung eine
maximale Lateralkraft von 0,1–1 nN resultiert. Bei einer für AFM-Spitzen
gebräuchlichen Federkonstanten von etwa 0,1 N/m ergibt sich damit eine
Auslenkung von 10–100 Å, was auch für AFM-Messungen ein typischer
Wert ist. Bei höheren Auflagekräften werden auch längere Einlaufstreifen
festgestellt.
Nach dieser sehr groben Abschätzung, die nur der Veranschaulichung der Größenordnungen dienen soll, sollte k im Falle der extremen Einlaufstreifen von fast 100 Å Länge den Wert 0,1 N/m nicht überschreiten. Wie sehen solche weichen Tunnelnadeln aus?
Es wurden für alle STM-Messungen unter Zugbelastung geschnittene Platin- Iridium-Drähte als Nadeln verwendet. Auf mikroskopischer Skala entstehen dabei sehr zerklüftete Strukturen, wie die rasterelektronenmikroskopische Aufnahme eines 13 µm × 16 µm großen Bereichs eines Nadelendes in Abbildung 6.9
|
|
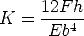 | (6.1) |
gegeben, wobei F die bei h = 0 wirkende laterale Kraft, E die Elastizitätskonstante und b die Breite des Balkens sind. Die mittlere Krümmung ist bei einem Balken der Länge L also
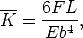 | (6.2) |
die so genäherte seitliche Auslenkung 
x, die klein gegen L sein soll, damit
![[ ---]
Dx = -1-. 1 - cos(L K) ,
K](main191x.jpg) | (6.3) |
wie man sich anhand einer kleinen Skizze leicht überlegen kann.
Da bei kleinen Auslenkungen der Krümmungsradius r = 1/K groß im Vergleich zu L ist, kann die Kosinusfunktion durch die ersten beiden nichtverschwindenden Glieder ihrer Reihenentwicklung ersetzt werden, woraus eine Federkonstante von
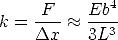 | (6.4) |
resultiert.
Da keine Information über die Elastizitätskonstante des zu 80 % aus Platin
bestehenden Drahtes vorlag und die hier gemachten Schätzungen ohnehin sehr grob
sind, wird für E diejenige reinen Platins verwendet, welche mit 168 GPa angegeben
wird [44]. Setzt man nun diese Größe sowie die Werte L = 1 µm und b = 0,5 µm,
die man an der in Abbildung 6.9 markierten Stelle abmißt, in Gl. 6.4
ein, so erhält man das Ergebnis k 3500 
, also eine zu harte Feder, um
Einlaufstreifen von 100 Å Länge zu erklären. Erst eine sehr viel längere und/oder
schmälere Faser als die unter dem Rasterelektronenmikroskop gefundene
würde eine genügend kleine Federkonstante liefern. Sie dürfte —um ein
Beispiel zu geben— bei einer Länge von 0,5 µm nicht dicker als 0,04 µm sein.
Angesichts solch zerklüfteter Spitzen könnten solche Fasern vielleicht gerade mit
ebenso großer Häufigkeit vorkommen, wie extreme Einlaufstreifen beobachtet
werden.
Eine äquivalente Erklärung wäre auch für das STM plausibel, da hier ebenfalls für die Spitze Potentialgräben anzunehmen sind. Abbildung 6.10
|
a)
|
Schon auf Bild 6.8d und 6.10b ist zu sehen, daß untere und obere Bildhälfte nicht äquivalent sind: Jeweils unten sind sogenannte y-Einlaufstreifen vorhanden. Abbildung 6.11
|
a)
|
|
a)
|
Vermutlich ist dies mit ein Grund für die große Variationsbreite der Charaktere von STM-Bildern. Die in diesem Kapitel dargestellten Ergebnisse lassen aber auch die Annahme zu, daß viele weitere Faktoren, die eine Asymmetrie im Bezug zur z-Achse bewirken, maßgeblichen Einfluß auf den Abbildungsprozeß haben, die da wären:
Obwohl viele Ähnlichkeiten zwischen zwischen AFM- und STM-Bildern bestehen, und so nach dem zueinander analoge Erklärungsansätze bieten, sollte doch betont werden, daß es einen entscheidenden Unterschied gibt: Während beim AFM/LFM direkt die Kräfte detektiert werden, liefert beim STM der Strom (bzw. die Rückkopplung des Regelkreises im CCI-Modus) das Meßsignal, welches nicht zwangsläufig mit lateralen Kräften korreliert sein muß. Zum Beispiel bedingt ein fast immer vorhandener, von lateralen Kräften herrührender Signalanteil beim AFM eine Scanhysterese. Der beim STM gemessene Tunnelstrom sollte jedoch unabhängig vom Vorzeichen der lateralen Kraft sein und somit keine Hysterese bilden. Trotzdem gelegentlich beobachtete Differenzen zwischen Hin- und Rücklauf könnten einerseits auf eine Asymmetrie des vordersten Spitzenteils, andererseits auch auf eine Verbiegung der Spitze, deren vordere und hintere Flanke verschiedene Tunneleigenschaften haben, zurückgeführt werden, wie in Abschnitt 6.2.1 beschrieben.
b)
c)
b)
c)
b) 
b)
c)
c)
e)
d)
f)
b)
c)
b)
b)