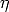4.1 Das Scheibchenmodell

4.1. Das Scheibchenmodell

Um STM-Bilder zu simulieren, muß zu jedem gewünschten Bildpunkt an dem zugehörigen Ort der Probenoberfläche der Tunnelstrom berechnet werden.

Zu Beginn der Suche nach den Mechanismen, die für die Kontrastinversion verantwortlich sind, wurde die Probenoberfläche durch eine zweidimensionale Fläche repräsentiert, auf der als hexagonales Gitter Kreisscheiben angeordnet sind, auf denen die Tunnelwahrscheinlichkeit den Wert 1 annimmt und sonst verschwindet. Der wesentliche Parameter für eine solche Modelloberfläche ist das Verhältnis vom Kreisradius zur Gitterkonstanten 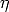= r/g. Abbildung 4.1

Abbildung 4.1:

Generierte Tunnelwahrscheinlichkeitsverteilung

(x,y) für eine hexagonale Oberfläche.

zeigt eine solche Tunnelwahrscheinlichkeitsverteilung

(x,y), die im folgenden Probenfunktion genannt wird, mit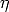

= 7/20.

Die Tunnelspitze wird ebenfalls durch eine zweiparametrige Funktion, nämlich (x,y), dargestellt, deren Wert auf einer Kreisscheibe mit dem Radius R und dem Mittelpunkt bei x = 0, y = 0 eins annimmt und sonst Null.

Der Tunnelstrom I(x_S,y_S) —wobei die Koordinaten x_S,y_S sich auf den Mittelpunkt der Spitzenscheibe beziehen— sei nun proportional zur Fläche unter der Spitzenscheibe, auf der = 1 gilt, wenn man die Ebene, die die Spitze repräsentiert, über die Probenfläche legt, und damit zur Korrelationsfunktion

integral integral dx dy t (x, y) s(x + x ,y + y ). S S

(4.1)

Abbildung 4.2

a) b)

Abbildung 4.2:

Auf der Basis des Scheibchenmodells simulierte Tunnelstrombilder: für die Modelloberfläche wurde

= 2/5 gewählt. Bei der kleinen Spitze (a) ist R/g = 3/20, bei der großen (b) 7/10. Die Erläuterung dieser Größen erfolgt im Text.

zeigt die Resultate der numerischen Auswertung des obigen Integrals für zwei verschiedene Werte von R. Der Rand des Bildes gibt die Probenfunktion

(x,y), also die Modelloberfläche wieder, während in der linken oberen Ecke jedes Bildes eine quadratische Fläche zu sehen ist, die die jeweilige Spitzenfunktion

(x,y) repräsentiert. Auf diese Weise kann man sich leicht veranschaulichen, wie die Spitze über die Oberfläche gerastert wird und dabei an jedem Punkt x_S,y_S der Strom berechnet wird. Wählt man nun R sehr klein, so ist anschaulich klar, daß I(x,y) die Modelloberfläche fast identisch wiedergibt, wie es Abbildung 4.2a bestätigt, wo das Verhältnis von R zu g 3-
20

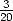beträgt: Das generierte Tunnelstrombild zeigt wie die Modelloberfläche ebenfalls runde Helligkeitsmaxima, die auch die gleichen Positionen einnehmen.

Für größer werdende Verhältnisse R/g ändert sich der Bildcharakter: in bestimmten Wertebereichen für R/g erhält man Kontrastinversion: an den Positionen der ursprünglichen Helligkeitsmaxima auf der Modelloberfläche erscheinen in der generierten Tunnelstromverteilung nun Minima. Die Abbildung 4.2b zeigt genau diesen Effekt.¹ Er kommt dadurch zustande, daß die Überlappung der Spitzenscheibe mit den Oberflächenkreisen zwischen den Gitterpunkten wegen mehrerer beteiligter Leitfähigkeitsmaxima größer als genau über einem Gitterpunkt ist, wo nur ein Leitfähigkeitsmaximum zur Korrelation und damit zum Strom beitragen kann.

Mittels dieses äußerst einfachen Modells ist es also bereits gelungen, ein anschauliches Verständnis von einem möglichen Mechanismus zur Entstehung der Kontrastinversion zu erhalten.

Welche Bedeutung hat jedoch die Spitzenscheibe? Und darf man die Oberfläche überhaupt so annähern? Bedenken könnten nicht nur darin liegen, Atome durch Kreisscheiben zu ersetzen, sondern auch in der Methode den Tunnelstrom zu berechnen, was hier durch die Korrelationsfunktion 4.1 geschieht.

Durch diese Fragen motiviert hat M. Epple in [18] ein weiteres Modell vorgestellt. Dieses soll vor allen Dingen auch dem Einfluß des Abstands zwischen Nadel und Oberfläche gerecht werden, der hier ja noch völlig fehlte.

[next] [front] [up]