4.2 Erste Modifikation des Modells

4.2. Erste Modifikation des Modells

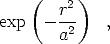
Wie im vorherigen Teil klar wurde, kann das Phänomen der Kontrastinversion leicht durch Simulationsrechnungen im Rahmen eines einfachen geometrischen Modells generiert werden, doch entspricht das oben vorgestellte Modell bei weitem noch nicht der physikalischen Realität. Die nächste Anpassung an die Physik besteht darin, die Oberfläche nicht mehr durch eine zweidimensionale Stufenfunktion, deren Wert 0 oder 1 ist, darzustellen, sondern durch hexagonal verteilte zweidimensionale Gaußfunktionen, deren Mittelpunkte auf den Gitterpunkten liegen, da man dadurch weiterhin einen Parameter behält, der den Radius der Atome angibt, nämlich a in dem Ausdruck

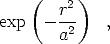( ) r2- exp - a2 ,

(4.2)

wobei r der Abstand zum nächstliegenden Gitterpunkt bzw. Atom ist.²

Außerdem wird nun eine punktförmige Spitze angenommen. Um nun den Gesamtstrom von der Oberfläche zur Nadel (oder umgekehrt³) zu berechnen, müssen die Ströme, die von allen Flächenelementen ausgehen, aufsummiert werden. Dazu wird für die Berechnung jedes einzelnen Teilstroms Gleichung 2.9 herangezogen. Dabei wird von folgenden Annahmen ausgegangen:

Die einzelnen Teilströme können als unabhängig voneinander angesehen werden.
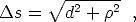
Die mittlere Barrierenhöhe, die in Gl. 2.9 als eingeht, soll konstant sein, also unabhängig vom Abstand s der Elektroden, der in diesem Fall einfach mit dem Satz des Pythagoras berechnet werden kann: $V~ ------- Ds = d2 + r2 ,$
wobei hier d der Spitze-Probe-Abstand ist und der Abstand des betrachteten Flächenelements von der senkrechten Verbindunglinie zwischen Spitze und Probe ist.
Die einzige variable Eigenschaft der Oberfläche sei die Tunnelwahrscheinlichkeitsverteilung, die durch die Probenfunktion (x,y) bestimmt wird, das heißt, daß die Modelloberfläche wiederum zweidimensional, ohne Höhenprofil, ist.

Ein Vorteil der letzten Annahme liegt darin, daß man den Algorithmus für die numerische Summation der Teilströme derart vereinfachen kann, daß die Rechenzeit drastisch verkürzt wird: anstatt für jeden Punkt (x_S,y_S), über dem sich die Nadel gerade befindet, die vollständige Summation auszuführen, wird bei der Simulation zuerst die Stromverteilung für eine strukturlose Oberfläche (also mit (x,y) = konstant) bis zu einem Radius _max berechnet.⁴ Das heißt, daß man bei vorgegebenen Parametern Abstand d₀ sowie mittlerer Barrierenhöhe ein einziges Mal

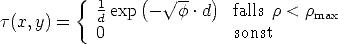{ 1 ( V~ -- ) t(x,y) = d exp - f .d falls r < rmax 0 sonst

(4.3)

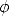
zu Beginn der Simulation berechnet, wobei zur Vereinfachung 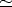1,05 ^. -12
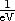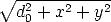Å 1eV ^. und d = V~ ------------
d20 + x2 + y2 eingeführt wurden.⁵ Dann muß nur noch für jeden Punkt (x_S,y_S) die Korrelationsfunktion (siehe Gl. 4.1) auswertet werden.

Abbildung 4.3

Abbildung 4.3:

Ein mit dem im Text beschriebenen Modell erzeugtes STM-Bild, auf dem man den Effekt der Kontrastinversion erkennen kann. Es wurden folgende Parameter, deren Bedeutung aus dem Text hervorgeht, gewählt:

= 2 eV, d₀ = 3 Å, g = 2,5 Å,

_max = 2 Å und a = 1 Å

zeigt ein Beispiel einer solchen Simulation. Die Parameter sind in den Bildunterschriften angegeben. Es wurde hier in die linke obere Ecke der relevante Ausschnitt von

(x,y), nämlich genau ein Quadrat, das den nicht verschwindenden Bereich der Funktion komplett einschließt, angeordnet. Der Rand, dessen Breite gerade

_max ist, gibt die ursprüngliche Oberfläche wieder und das innere Scanfenster das simulierte Strombild I(x,y). Die Abklinglänge a der Gaußschen Funktion 4.2 wurde —bei einer Gitterkonstanten von 2,5 Å— gleich 1 Å gesetzt, da sich bei den verschiedenen Simulationsreihen herausgestellt hatte, daß ein zu kleiner Wert für a lediglich an jedem Gitterpunkt ein Abbild von der Funktion

erzeugte und ein zu hoher wiederum die „Welligkeit“ der Oberfläche verschwinden ließ. Das bedeutet, daß eine beliebige Variation dieses Parameters nicht als sinnvoll erachtet werden kann, wie es z.B. bei dem Abstand d₀ der Fall ist. Im nächsten Abschnitt wird die Modelloberfläche auf eine andere Weise realisiert.

Folgende Ergebnisse wurden durch die Simulationen mit diesem Modell, welches auf einer punktförmigen Spitze und „gaußförmigen“ Oberflächenatomen basiert, erzielt:

Weiterhin, wie schon beim Scheibchenmodell, werden invertierte Tunnelstrombilder (siehe Abb. 4.3) erzeugt. Doch wird hier anstelle des „Spitzenscheibendurchmessers“ der Abstand variiert. Es wird eine Äquivalenz zwischen d₀ und dem Durchmesser 2R der Spitzenscheibe beim Scheibchenmodell beobachtet, die folgendermaßen erklärt werden kann: Bei kleinen Abständen fließt der Hauptanteil des Elektronenstroms aus dem Bereich, der unmittelbar unter der Spitze liegt. Weiter entfernte Gebiete verlieren aufgrund der exponentiellen Abhängigkeit des Tunnelstroms von der Tunnellänge schnell an Einfluß: die effektive Fläche der Spitze ist so klein, daß die Situation der in Bild 4.2a dargestellten nahekommt. Steigt der Abstand, so steigt auch die Gewichtung bezüglich des Tunnelstroms der weiter außen liegenden Bereiche: die Funktion (x,y), so wie sie in Abb. 4.3 in der linken oberen Ecke zu sehen ist, wird innerhalb x² + y² < _max² flacher, nähert sich also der Kreisscheibe an, auf der die Tunnelwahrscheinlichkeit konstant gleich eins ist.
Wie auch bei den Simulationsrechnungen des Scheibchenmodells ergibt sich hier ebenfalls, daß auf die erste Kontrastinversion nach weiterer Steigerung diesmal des Abstands —beim Scheibchenmodell war es der Spitzenradius— wieder ein Bereich nichtinvertierter Bilder folgt, usw. Dies kann auf dieselbe Art wie oben erklärt werden.
Die simulierten Bilder sind stark vom gewählten Parameter _max abhängig: bei der Simulationsrechnung für Abbildung 4.3 wurde er auf 2 Å gesetzt, doch ist diese Wahl willkürlich und wird in den folgenden Abschnitten noch ausgiebig diskutiert werden.

Allerdings blieben auch hier noch einige Fragen offen. Gerade der letzte Punkt muß noch weiter analysiert werden, denn konsequenterweise muß hier immer soweit integriert werden, bis eine Konvergenz der Ergebnisse eintritt. Das soll im folgenden noch geschehen.

Zusätzlich wird im nächsten Teil außer der Probenfunktion, die die Tunnelwahrscheinlichkeitsverteilung darstellt, auch die dreidimensionale Struktur der Oberfläche mit einbezogen, anstatt die Probe weiterhin als planare Elektrode zu betrachten.

[next] [prev] [prev-tail] [front] [up]