[next] [tail] [up]

A.1.  Integration der Transmissionswahrscheinlichkeit T(Ex)

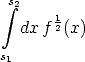
Den Ausführungen im Anhang von [37] folgend, läßt sich das Integral der Quadratwurzel einer beliebigen Funktion f(x)

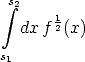integral s2 dx f12(x) s1
(A.1)

vereinfachen, indem man

{ [ ]} -f(x)---f-- f(x) = f 1 + f
(A.2)

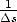
schreibt, wobei 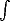f = -1- Ds integral s1s2dx f(x) definiert wird.

Man setze nun Gl.  A.2 in das Integral  A.1 ein und entwickle den Ausdruck in (f(x) -f )/f . Unter Vernachlässigung von Termen mit [ ] (f(x) - f)/f3 und höheren Ordnungen erhält man damit

{ } integral s2 1 1 integral s2 [f(x) - f] [f (x)- f]2 dx f2(x) -~ f 2 dx 1 + ------------ ------------ . 2f 8f 2 s1 s1
(A.3)

Das Integral des zweiten Terms verschwindet per definitionem, so daß

integral s2 1 1 { 1 integral s2 [ ]2} dx f2(x) -~ f 2Ds 1 - ------- dx f (x)- f 8f 2Ds s1 1 s1 = bf 2Ds, (A.4)
wobei Ds = s2 - s1. Es wurde der Korrekturfaktor
s2 1 integral [ ]2 b := 1 - --2---- dx f(x) - f 8f Ds s1
(A.5)

eingeführt. Gewöhnlich gilt 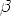b ~~ 1, so daß

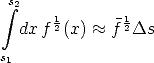integral s2 1 1 dx f 2(x) ~~ f 2Ds s1
(A.6)

eine gute Näherung darstellt.

Ersetzt man nun f(x) durch (EF + 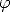f - Ex), so wird aus Gleichung  2.2

{ V ~ ------------} T(Ex) -~ exp - ADs EF + f - Ex .
(A.7)

Für V (x) wurde hier EF + 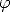f eingesetzt. Außerdem führten wir als Abkürzung

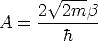
2V ~ 2mb A = -------- h

ein.

[next] [front] [up]