
Um zu dem Ausdruck 2.8 für die Tunnelstromdichte J zu gelangen, hat John G. Simmons die Größen
 | (A.8) |
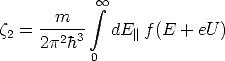 | (A.9) |
und
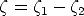 | (A.10) |
eingeführt, mit denen sich
(siehe Gleichungen 2.1 und 2.5) zu
 | (A.12) |
vereinfachen läßt.
Bei 0 Kelvin sind  1 und
1 und  2 durch
2 durch
 | (A.13) |
und
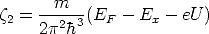 | (A.14) |
gegeben. Auf diese Weise erhalten wir
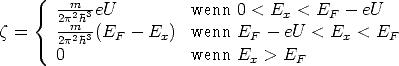 | (A.15) |
Gleichungen A.7 und A.15 in Gl. A.12 eingesetzt ergibt die Tunnelstromdichte J, wie sie in Gleichung 2.7 ausgedrückt ist:
Simmons zeigt in [37], wie Gl. A.16 integriert werden kann, wenn man sie in folgender Form schreibt: Das erste Integral ergibt Der zweite Term, in dem die Fermienergie im Exponenten steht, ist gegenüber dem ersten vernachlässigbar. Da zusätzlich A s(
s( + eU)
+ eU)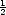 » 1 gilt, reduzieren wir das
Ergebnis A.18 zu
» 1 gilt, reduzieren wir das
Ergebnis A.18 zu
![1 [ 1]
(8pme2/h3ADs)U (f + eU )2 exp - ADs(f + eU)2 .](main233x.jpg) | (A.19) |
Genauso wie das erste, so kann auch das zweite Integral behandelt werden:
Das dritte Integral der Gleichung A.17 hat die Form
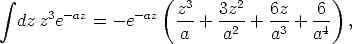 | (A.21) |
wenn man z2 = E
F +  - Ex substituiert.
- Ex substituiert.
Wenn die letzten beiden Terme in der Klammer von Gleichung A.21 gegenüber den beiden vorangehenden vernachlässigt werden, berechnet sich das dritte Integral in Gleichung A.17 zu
Aus der Summation über die drei Teilergebnisse A.19, A.20 und A.22 resultiert
![{ 1 [ 1]}
J = J0 fexp( - ADsf 2)- (f + eU) exp -ADs(f + eU )2 ,](main238x.jpg) | (A.23) |
wobei
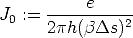 | (A.24) |
definiert wurde.
Für kleine Spannungen, d.h. eU « , nimmt
, nimmt 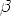 , wie in Gleichung A.5 definiert,
den Wert eins an. Außerdem läßt sich Gl. A.23 durch weitere Näherungen
vereinfachen: zuerst kann im Argument der zweiten Exponentialfunktion die Wurzel
entwickelt werden, so daß wir
, wie in Gleichung A.5 definiert,
den Wert eins an. Außerdem läßt sich Gl. A.23 durch weitere Näherungen
vereinfachen: zuerst kann im Argument der zweiten Exponentialfunktion die Wurzel
entwickelt werden, so daß wir
![[ ( 1)] ( 1)
J = J0 f - (f + eU )exp - ADseU/2f 2 .exp -ADsf 2](main241x.jpg) | (A.25) |
erhalten. Werden Terme in U2 und höheren Ordnungen der Taylorreihe aus
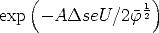
vernachlässigt, so geht Gl. A.25 in
über. Dies läßt sich wegen A s
s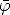
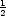 /2 » 1 zu
/2 » 1 zu
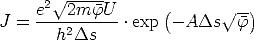 | (A.27) |
reduzieren.