3.5. Cristallisation des couches déposées amorphes par SPC
Cette section aborde l’étude de la cristallisation des couches déposées amorphes par
la méthode SPC (voir page 32). La cristallisation est suivie par la mesure in situ de
la conduction de la couche comme expliqué en détail dans l’annexe A.2. Nous
essayerons d’abord d’interpréter l’évolution du courant électrique à travers
la couche, pour ensuite évaluer l’influence des conditions de dépôt sur la
cristallisation.
3.5.1. Interprétation de la conductivité pendant le recuit
Une allure
caractéristique de l’évolution en fonction du temps du courant à tension constante
pendant le recuit isotherme, est donnée sur la figure 3.7.

| FIG. 3.7: | Courbe typique de l’évolution de la conductivité pendant la
cristallisation. La mesure expérimentale peut être approximée par les trois
droites tracées en rouge définissant les temps caractéristiques tn et tf. |
|
Au début la conductivité augmente légèrement ou reste pratiquement constante
jusqu’à t = tn, puis elle augmente et atteint sa valeur maximale à t = tf.
Ce comportement peut s’expliquer de la façon suivante. La cristallisation
commence à l’interface entre le substrat et la couche, comme cela a été déjà montré
pour des couches déposées par LPCVD en se servant d’images de microscopie
électronique à transmission [89]. Au début, dès l’apparition des premiers germes à
l’interface et leur croissance supposée hémisphérique, le courant augmente
seulement légèrement jusqu’à leur coalescence, qui donnera lieu à une couche
continue polycristalline. Ce moment est considéré comme équivalent à tn. À partir
de là, ces grains vont continuer à croître vers la surface d’une manière collonnaire,
et le courant monte plus rapidement jusqu’à t = tf. Une bonne corrélation entre
la fraction cristalline et l’allure du courant a été d’ailleurs démontré par
King KIS-SION [61] toujours pour du silicium déposé par LPCVD en suivant
également la cristallisation par des mesures de diffraction de rayons X in
situ.
Avec cette image simplifiée de la croissance des grains, c’est-à-dire une croissance
unidirectionnelle de l’interface vers la surface, on peut établir la relation
linéaire A.2 (page 282) entre le taux cristallin et la conductivité. Pour
cette raison, la courbe est approchée par trois droites (tracées en rouge
dans la figure 3.7) permettant de trouver aisément les paramètres tn et
tf.
La vitesse de croissance des grains devient donc
 | (3.5) |
avec l’épaisseur de la couche d. Le « temps de nucléation » tn est un paramètre,
qui est inversement proportionnel au taux de nucléation, puisque la coalescence des
cristallites est d’autant plus retardée, que leur densité est faible.
Pour confirmer l’hypothèse, que nos couches cristallisent
dans ce mode bidimensionnel, des mesures de spectroscopie
RAMAN9
ont été effectuées sur quelques échantillons partiellement cristallisés. C’est-à-dire
que le recuit a été arrêté entre tn et tf. Ces échantillons ont été éclairés
successivement par deux faisceaux LASER de longueur d’onde différente sur la face
avant et sur la face arrière, c’est-à-dire à travers le verre. Puisque la pénétration de
la lumière est moindre à plus haute fréquence, on peut sonder des volumes différents
avec les deux faisceaux LASER. Ceci est illustré par les valeurs de profondeur de
pénétration x dans le tableau 3.4 :
| TAB. 3.4: | Profondeur de pénétration x en µm pour laquelle 63 % de l’intensité
de la lumière est absorbée. |
 | silicium amorphe | silicium cristallin
| | 514,5 nm | 0,1 | 0,9 |
| 457,9 nm | 0,033 | 0,4 |
| |
|
|
à la longueur d’onde  = 514,5 nm (LASER vert), x est deux à trois fois plus élevé
qu’à
= 514,5 nm (LASER vert), x est deux à trois fois plus élevé
qu’à  = 457,9 nm (LASER violet). La figure 3.8
= 457,9 nm (LASER violet). La figure 3.8
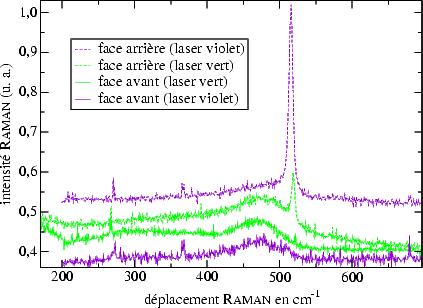
| FIG. 3.8: | Quatre spectres de l’intensité RAMAN en fonction du déplacement
RAMAN : les deux courbes au dessus sont mesurées sur la face avant et les
deux au dessous sur la face arrière avec respectivement un faisceau LASER vert
( = 514,5 nm) et violet ( = 514,5 nm) et violet ( = 457,9 nm). = 457,9 nm). |
|
montre les spectre RAMAN pour ces quatre cas de mesures sur un échantillon d’une
épaisseur de 2,5 µm, recuit à 570 ℃ : en éclairant par la face avant on ne détecte
quasiment aucun pic à environ 521 cm-1 —caractéristique de la phase cristalline du
silicium—, par contre la bosse autour de 480 cm-1 —caractéristique pour la phase
amorphe— est bien visible. Quand la couche est éclairée par la face arrière, le pic
cristallin est observé. Il est plus intense par rapport au pic amorphe, avec le
LASER violet. Cette asymétrie conforte notre hypothèse d’une nucléation à
l’interface.
Il est évident, que le mode de cristallisation dépend de la température de recuit.
Pour cette raison, cette expérience a été refaite avec des recuits à 600 et 630 ℃ : le
résultat reste le même !
3.5.2. Influence des paramètres de dépôt sur la vitesse de croissance des
grains
Nous avons effectué des suivis de conductance pendant le recuit pour
plusieurs séries d’échantillons, afin de mettre en évidence un éventuel impact de la
température ou de la pression de dépôt sur la vitesse de croissance des grains V c.
Celle-ci a toujours été déterminée selon l’équation 3.5. Sur la figure 3.9
sont représentées les valeurs V c en fonction de la température de dépôt, pour une
pression totale de 50 mbar (figure 3.9a) et pour une pression plus élevé
P = 400 mbar (figure 3.9b).
On remarque, que V c augmente avec Td pour une basse pression de dépôt, ce qui
n’est plus le cas pour une pression plus élevée P = 400 mbar où V c atteint un
maximum à Td = 560 ℃ pour ensuite rediminuer.
En traçant V c en fonction de la pression totale de dépôt P, comme le montre la
figure 3.10
pour Td = 540 ℃ (a) et Td = 620 ℃ (b), on remarque un comportement
similaire que l’on peut résumer ainsi : V c augmente en général avec la pression P,
jusqu’à une valeur maximale, qui dépend de la température de recuit Tc, pour
ensuite rediminuer.
Par ailleurs, selon [59], V c est activé thermiquement et suit l’équation
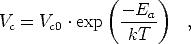 | (3.6) |
où Ea dépend de la densité de défauts structuraux dans le silicium amorphe : plus
ces derniers sont nombreux, plus l’énergie d’activation est élevée. V c0 dépend du
coefficient de capture des liaisons pendantes et augmente avec la concentration de
liaisons pendantes chargées.
Lorsque V c pour un jeu de paramètres de dépôt fixe, suit une telle allure
exponentielle,10
on peut déduire l’énergie d’activation de la cristallisation pour nos couches :
elle varie entre 2,3 eV et 3,1 eV. Dans la littérature on trouve des valeurs
similaires variant de 2,4 eV [61, 139] à 2,7–2,9 eV [11, 73]. Ces différentes
valeurs semblent correspondre à différentes micro-structures du silicium
amorphe [61].
Grâce à la variation importante de l’épaisseur de nos couches un phénomène
intéressant devenait visible : V c ne dépend pas seulement de la structure amorphe
initiale, mais aussi de l’épaisseur de la couche, comme il est illustré par la figure
3.11.
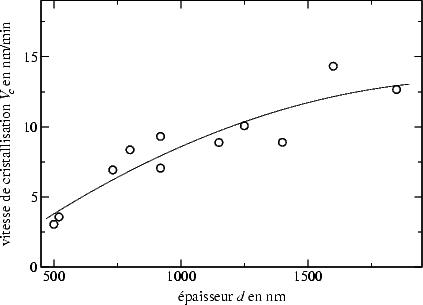
| FIG. 3.11: | Variation de la vitesse de cristallisation V c en fonction de
l’épaisseur d de la couche pour des conditions de dépôt diverses. |
|
En effet, la cristallisation semble s’accélérer, puisque V c croit avec l’épaisseur. Ceci
est probablement dû à des orientations de grains différentes. Il est connu en effet,
que les vitesses de cristallisation dépendent fortement de l’orientation : la
croissance la plus rapide se fait dans la direction (100). La croissance dans les
directions (113), (110), (112) et (111) est respectivement 3/2, 3, 5 et 24 fois plus
lente [120].
On considère en général deux phases de cristallisation : la croissance des
germes à l’interface dans les trois dimensions jusqu’à leur coalescence, et puis
une croissance collonnaire bidimensionnelle vers la surface [9, 61, 139].
En introduisant une troisième phase, comme schématisé dans la figure
3.12,
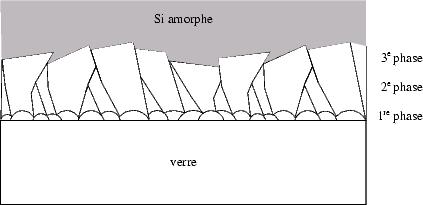
| FIG. 3.12: | Modèle de croissance de grains pendant le recuit par SPC : pendant
une 1re phase les germes coalescent, la 2e phase consiste à une cristallisation
approximativement perpendiculaire à la surface, tandis que les grains avec un
V c plus élevé suppriment la croissance d’autres grains dans une 3e phase. |
|
il est possible d’interpréter ce phénomène. Au début, les germes naissent à
l’interface du silicium avec le verre, puis croissent pendant une première phase
jusqu’à leur coalescence. Ce moment correspond à tn comme définit sur la page 109
(figure 3.7). Il n’existe aucune orientation préférentielle de ces grains, comme c’est
également le cas dans la deuxième phase, où ils vont croître vers la surface.
Cependant, pendant cette phase, les différentes vitesses de croissance selon les
orientations cristallines entraînent une suppression de certains grains en
faveur d’autres. Il s’en suit l’existence d’une troisième phase, où la vitesse
de croissance est plus élevée qu’avant avec des grains d’une orientation
prépondérante.
Dans le but d’évaluer cette hypothèse, nous avons déterminé les facteurs
d’orientation Ohkl par des mesures de diffraction X d’après la méthode
décrite dans l’annexe A.4.3, pour trois échantillons d’épaisseur 200 nm,
1450 nm et 4300 nm respectivement. Les résultats sont reportés sur la figure
3.13

| FIG. 3.13: | Facteurs d’orientation Ohkl des cinq raies les plus intenses pour
trois échantillons d’épaisseurs différentes. |
|
où l’on note, que tous les échantillons montrent une faible texture de direction
(422) ; ce qui est aussi le cas pour les couches déposées par LPCVD [89].
On observe cependant un volume cristallin d’orientation (422) environ 5 % plus
élevé pour l’échantillon de forte épaisseur, que pour celui de seulement 200 nm
d’épaisseur. En même temps le volume correspondant à l’orientation (111)
diminue fortement avec un d croissant. Un léger changement d’orientation
prépondérante, qui peut étayer notre modèle, est donc visible. Il est clair, que les
grains, qui entrent en jeu dans la troisième phase de la croissance, ont une
orientation préférentielle par rapport à leur direction de croissance, mais pas
forcement par rapport à la surface : les grains peuvent croître d’une manière
diagonale.
D’après notre modèle, nous nous attendons également à une augmentation de la
taille de grains avec la distance par rapport au substrat. Afin d’évaluer cette
hypothèse, nous avons préparé deux échantillons du même dépôt d’épaisseurs
différentes11
avec la solution de SECCO [111], qui consiste en du bichromate de potassium (KCr2O7)
dilué dans l’eau avec de l’HF et qui attaque en priorité le silicium amorphe, donc les
joints de grains. Après un dépôt très mince (50 Å) d’aluminium par évaporation
thermique, les surfaces de ces échantillons ont été visualisées en utilisant le
MEB12 du
GMV. Les photos obtenues sont présentées sur la figure 3.14 :
les structures visualisées ont des dimensions nettement plus grandes pour la
couche d’épaisseur de 2 µm, que celles de la couche amincie.
Nous avons également observé une conductivité électrique variant en fonction de
l’épaisseur. La figure 3.15
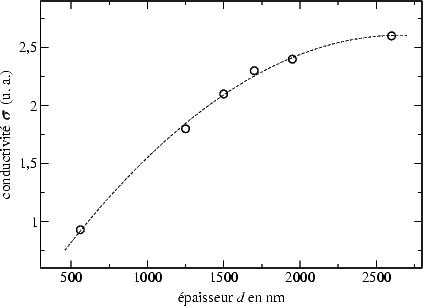
| FIG. 3.15: | Conductivité électrique  d’une couche de Si-poly en fonction de
son épaisseur d. d’une couche de Si-poly en fonction de
son épaisseur d. |
|
présente cette variation. Les valeurs sont obtenues par une série de gravures sèches à
l’aide d’un plasma de SF6 de la même couche afin de l’amincir et des mesures
d’épaisseur par TALYSTEP et de conductivité par la méthode de quatre
pointes13
entre deux gravure consécutives. La plus faible conductivité pour la couche amincie
jusqu’à 560 nm peut être expliquée par une plus mauvaise qualité cristalline
proche de l’interface. Néanmoins, nous ne pouvons pas exclure un effet du
plasma même, qui peut dégrader la conductivité proche de la surface en
l’amorphisant.
3.5.3. Influence des paramètres de dépôt sur la vitesse de nucléation
D’après
notre modèle de cristallisation bidimensionnelle, l’épaisseur des couches et son
inhomogénéité ne devraient pas affecter le temps de nucléation tn ; ce qui est
confirmé par l’absence de variation de tn en fonction de d. Par contre, on observe
une variation selon les conditions de dépôt, comme le montre la figure 3.16,
où tn est tracé en fonction de 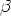 = 1/kTc en échelle semi-logarithmique. On
constate, que le temps de nucléation est thermiquement activé avec des énergies
d’activation résumées dans le tableau 3.5.
= 1/kTc en échelle semi-logarithmique. On
constate, que le temps de nucléation est thermiquement activé avec des énergies
d’activation résumées dans le tableau 3.5.
| TAB. 3.5: | Énergies d’activation du temps de nucléation pour toutes les
conditions de dépôt en électronvolt. |
| P (mbar) | 25 | 50 | 100 | 200 | 400 | 600 |
| Td = 540 ℃ | | | 3,4 | 3,2 | 2,8 | 3,1 |
| 560 ℃ | | 3,6 | 3,0 | 3,1 | 3,1 | 3,2 |
| 580 ℃ | 3,1 | 3,1 | 2,9 | 3,1 | 3,1 | |
| 600 ℃ | 2,8 | 2,9 | 3,1 | 2,9 | 3,6 | |
| 620 ℃ | 2,6 | 2,6 | 2,5 | | | |
| |
|
|
Plusieurs points peuvent être notés :
- pour de basses pressions totales (P < 200 mbar) l’énergie d’activation
Ea a tendance à diminuer lorsque la température de dépôt augmente,
tandis qu’à plus forte pression (P > 200 mbar) on observe une tendance
inverse ;
- à une pression fixe (figure 3.16a), le taux de nucléation augmente avec
Td ;
- pour une température de dépôt fixe (figure 3.16b) tn augmente avec P.
En considérant les résultats obtenus en section 3.4, nous pouvons interpréter
un temps de nucléation plus élevé en terme d’un contenu en hydrogène
plus important. En effet, pour la formation de germes, l’hydrogène doit
exodiffuser, ce qui retarde la nucléation. Néanmoins, il est également possible que
la structure du matériau amorphe soit plus irrégulière à haute vitesse et
basse température de dépôt demandant ainsi un temps de germination
plus longue. Cette dernière explication a été donnée aussi par HATALIS et
GREVE [47].



 = 514,5 nm (LASER vert), x est deux à trois fois plus élevé
qu’à
= 514,5 nm (LASER vert), x est deux à trois fois plus élevé
qu’à  = 457,9 nm (LASER violet). La figure 3.8
= 457,9 nm (LASER violet). La figure 3.8

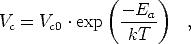




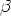 = 1/kTc en échelle semi-logarithmique. On
constate, que le temps de nucléation est thermiquement activé avec des énergies
d’activation résumées dans le tableau 3.5.
= 1/kTc en échelle semi-logarithmique. On
constate, que le temps de nucléation est thermiquement activé avec des énergies
d’activation résumées dans le tableau 3.5.